Independent Events
Independent Events: Overview
This topic covers concepts, such as, Independent and Dependent Events & Independency of Three or More Events etc.
Important Questions on Independent Events
Let denote the complement of an event . Let be pairwise independent events with and . Then equals
Two fair dice are rolled. Let be the event that the first die shows an even number and be the event that the second die shows an odd number. The two events and are:
A box contains four blue balls and three green balls. Judith and Gilles play a game with each taking it in turn to take a ball from the box, without replacement. The first player to take a green ball is the winner. Judith plays first. Find the probability that she wins. The game is now changed so that the ball chosen is replaced after each turn. Judith still plays first. Determine whether the probability of Judith winning has changed.
A box contains four blue balls and three green balls. Judith and Gilles play a game with each taking it in turn to take a ball from the box, without replacement. The first player to take a green ball is the winner. Judith plays first. Find the probability that she wins.
Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is . The probability that the second set of lights is green is . The probability that the third set of lights is green is . It may be assumed that the probability of any set of lights being green is independent of the others. Find the probability that at least one set of lights will be green.
Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is . The probability that the second set of lights is green is . The probability that the third set of lights is green is . It may be assumed that the probability of any set of lights being green is independent of the others.Given that first set of light is red and (i.e. not green), find the probability that the following two pairs of lights will be green.
Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is . The probability that the second set of lights is green is . The probability that the third set of lights is green is . It may be assumed that the probability of any set of lights being green is independent of the others. Find the probability that only one set of light is green.
Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is . The probability that the second set of lights is green is . The probability that the third set of lights is green is . It may be assumed that the probability of any set of lights being green is independent of the others. Find the probability that all three sets of light are green.
In a survey, people were asked about their holidays over the past year. It was found that people had taken a holiday in Europe, and people had taken a holiday in the USA.
Everyone surveyed had been taken holiday to at least Europe or the USA. Explain why the events "taking a holiday in Europe" and "taking a holiday in the USA" are not independent events.
and are independent events, such that and .
Find the probability .
and are independent events, such that and .
Find the probability .
and are independent events, such that and .
Find the probability .
and are independent events, such that and .
Find the probability .
A group of investors own properties in north European cities. The following Venn diagram shows how many investors own properties in Amsterdam, Brussels or Cologne. One of the investors is chosen at random.
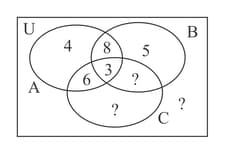
Find and Interpret your answers .
A supermarket uses two suppliers, and of strawberries. Supplier supplies of the supermarkets's strawberries. Strawberries are examined in a quality control inspection (): of the strawberries supplied by pass and of the strawberries from pass .
A strawberry is selected at random.
The supermarket wants the probability that a strawberry passes to be . Find the percentage of strawberries that should be supplied by in order to achieve this.
Find the percentage of strawberries that should be supplied by in order to achieve this is , then the value of is .....A supermarket uses two suppliers, and of strawberries. Supplier supplies of the supermarkets's strawberries. Strawberries are examined in a quality control inspection (): of the strawberries supplied by pass and of the strawberries from pass .
A strawberry is selected at random.
In a sample of strawberries, find the expected number of strawberry that would fail .
A supermarket uses two suppliers, and of strawberries. Supplier supplies of the supermarkets's strawberries. Strawberries are examined in a quality control inspection (): of the strawberries supplied by pass and of the strawberries from pass .
A strawberry is selected at random.
Find the probability that the strawberry passes .
(Round off and Write answer up to decimal places)
A class of undergraduate students were asked in their major subject and whether they listen to music on their commute to university. is the set of science majors and is the set of students who listen to music on their commute.
The same questions were asked in a survey in with the results given in the venn diagram below.
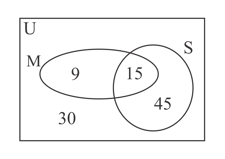
Find and and hence determine whether and are independent events, stating a reason for your answer.
The letters of the word are written on separate cards on shown below:
In a different experiment, a card is drawn at random and not replaced. Then another card is drawn.
Let be the event the first card drawn is the letter .
Let be the event the second card drawn is the letter . Find .
